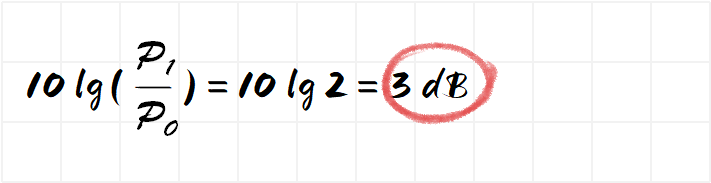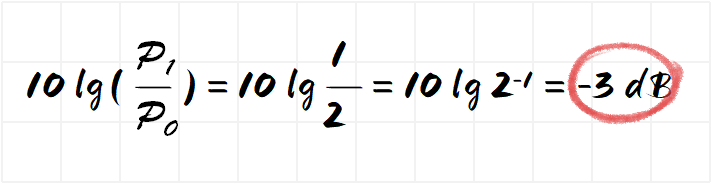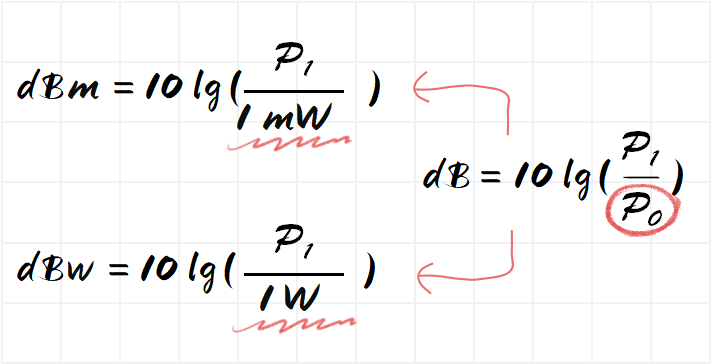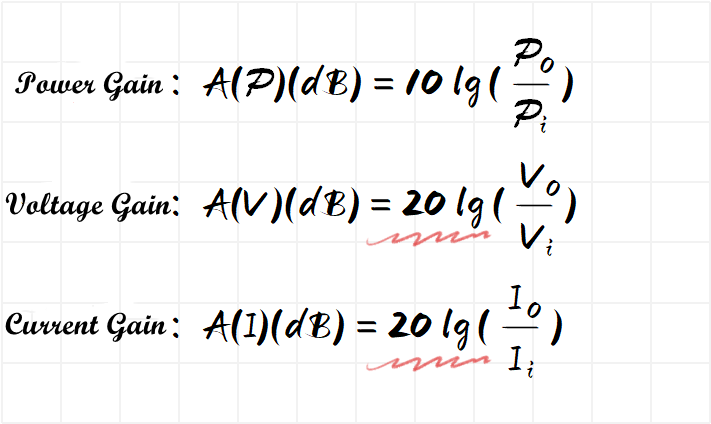How to explain and calculate dB, dBm, dBw...what is the difference between them?
dB should be the most basic concept in wireless communication. we often say “transmission loss is xx dB,” “transmission power is xx dBm,” “antenna gain is xx dBi” …
Sometimes, this dB X may be confused and even cause calculation errors. So, what is the difference between them?

The matter has to start with dB.
When it comes to dB, the most common concept is 3dB!
3dB often appears in the power diagram or BER (Bit Error Rate). But, in fact, there is no mystery.
A drop of 3dB means that the power is reduced by half, and the 3dB point means the half-power point.
+3dB means double the power, -3Db means the decrease is ½. How did this come from?
It is actually very simple. Let’s take a look at the calculation formula of dB:

dB represents the relationship between the power P1 and the reference power P0. If P1 is twice P0, then:
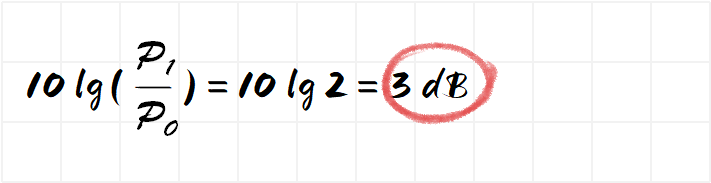
if P1 is half of P0, then,
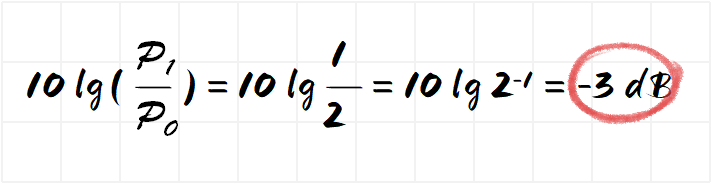
about the basic concepts and operation property of logarithms, you can review the mathematics of logarithms.
[Question]: The power is increased by 10time. How many dB there?
Please remember a formula here.
+3 *2
+10*10
-3 / 2
-10 / 10
+3dB means that the power is increased by 2 times;
+10dB means that the power is increased by 10 times.
-3 dB means that the power is reduced to 1/2;
-10dB means that the power is reduced to 1/10.
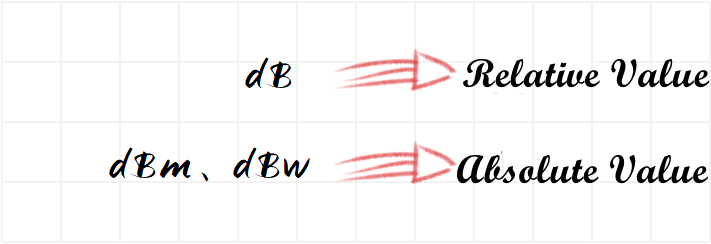
It can be seen that dB is a relative value, and its mission is to express a large or small number in a short form.
This formula can greatly facilitate our calculation and description. Especially when drawing a form, you can fill it up with your own brain.
If you understand dB, now, let’s talk about the dB family numbers:
Let’s start with the most commonly used dBm and dBw.
dBm and dBw are to replace the reference power P0 in the dB formula with 1 mW, 1W
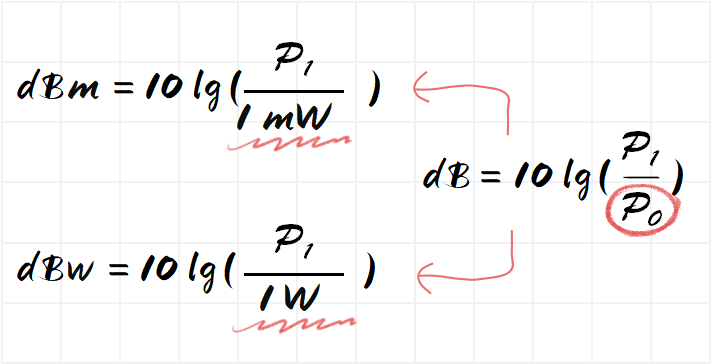
1mw and 1w are definite values, so dBm and dBw can represent the absolute value of power.
Following is the power conversion table for your reference.
| Watt | dBm | dBw |
| 0.1 pW | -100 dBm | -130 dBw |
| 1 pW | -90 dBm | -120 dBw |
| 10 pW | -80 dBm | -110 dBw |
| 100 pW | -70 dBm | -100 dBw |
| 1n W | -60 dBm | -90 dBw |
| 10 nW | -50 dBm | -80 dBw |
| 100 nW | -40 dBm | -70 dBw |
| 1 uW | -30 dBm | -60 dBw |
| 10 uW | -20 dBm | -50 dBw |
| 100 uW | -10 dBm | -40 dBw |
| 794 uW | -1 dBm | -31 dBw |
| 1.000 mW | 0 dBm | -30 dBw |
| 1.259 Mw | 1 dBm | -29 dBw |
| 10 mW | 10 dBm | -20 dBw |
| 100 Mw | 20 dBm | -10 dBw |
| 1 W | 30 dBm | 0 dBw |
| 10 W | 40 dBm | 10 dBw |
| 100 W | 50 dBm | 20 dBw |
| 1 kW | 60 dBm | 30 dBw |
| 10 kW | 70 dBm | 40 dBw |
| 100 kW | 80 dBm | 50 dBw |
| 1 MW | 90 dBm | 60 dBw |
| 10 MW | 100 dBm | 70 dBw |
We must remember:
1w = 30dBm
30 is the benchmark, which is equal to 1w.
Remember this, and combine the previous “+3 *2, +10*10, -3/2, -10/10” you can do a lot of calculations:
[Question] 44dBm = ? w
Here, we must note that:
Except for 30dBm on the right side of the equation, the rest of the split items must be expressed in dB.
[Example] If A's output power is 46dBm and the output power of B is 40dBm, it can be said that A is 6dB greater than B.
[Example] If antenna A is 12 dBd, the antenna B is 14dBd, it can be said that A is 2dB smaller than B.
For example, 46dB means that P1 is 40 thousand times P0, and 46dBm means that the value of P1 is 40w. There is only one M difference, but the meaning can be completely different.
The common dB family also have dBi, dBd, and dBc. Their calculation method is the same as the dB calculation method, and they represent the relative value of power.
The difference is that their reference standards are different. That is, the meaning of the reference power P0 on the denominator is different.
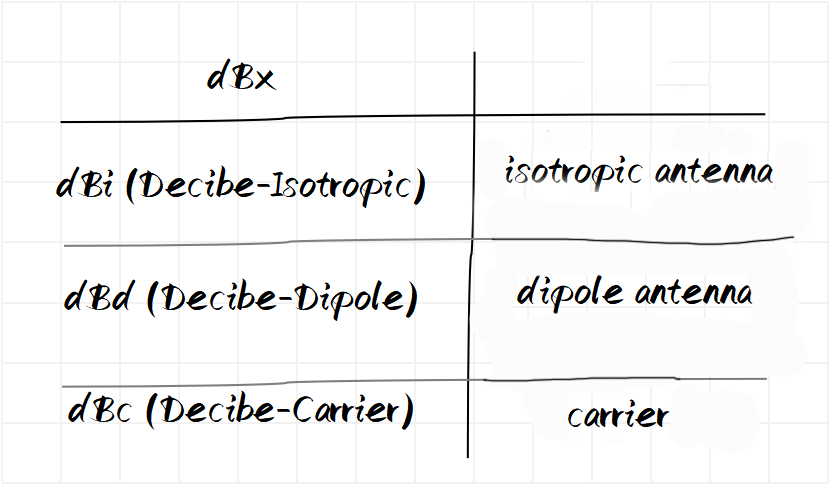
Generally, expressing the same gain, expressed in dBi, is 2.15 larger than expressed in dBd. This difference is caused by the different directivities of the two antennas.
In addition, the dB family can not only represent the gain and power loss but also represent voltage, current, and audio, etc.,
It should be noted that for the gain of power, we use 10lg(Po/Pi), and for the voltage and current, we use 20lg(Vo/Vi) and 20lg(Lo/Li)
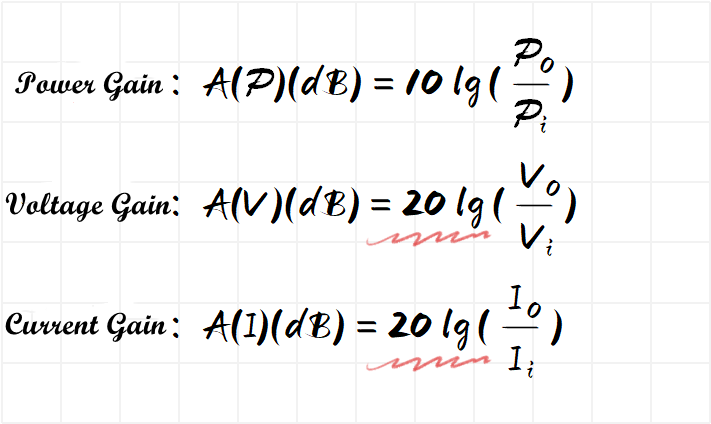
How did this 2 times more come from?
This 2 times is derived from the square of the electric power conversion formula. The n-the power in the logarithm corresponds to n times after calculation.

You can review your high school physics course about the conversion relationship between power, voltage, and current.
At last, I complied with some major dB family members for your reference.
Relative value:
| Symbol | Full Name |
| dB | decibel |
| dBc | decibel carrier |
| dBd | decibel dipole |
| dBi | decibel-isotropic |
| dBFs | decibel full scale |
| dBrn | decibel reference noise |
Absolute value:
Symbol | Full Name | Reference Standard |
| dBm | decibel milliwatt | 1mW |
| dBW | decibel watt | 1W |
| dBμV | decibel microvolt | 1μVRMS |
| dBmV | decibel millivolt | 1mVRMS |
| dBV | decibel volt | 1VRMS |
| dBu | decibel unloaded | 0.775VRMS |
| dBμA | decibel microampere | 1μA |
| dBmA | decibel milliampere | 1mA |
| dBohm | decibel ohms | 1Ω |
| dBHz | decibel hertz | 1Hz |
| dBSPL | decibel sound pressure level | 20μPa |
And, let’s check if you understand or not.
[Question] 1. The power of 30dBm is
[Question] 2. Assuming that the total output amount of the cell is 46dBm, when there are 2 antennas, the power of a single antenna is